- Photoelectric‧Electro-optical High Efficiency Conversion Materials
- Energy Storage and Catalytic Energy Materials
- Energy Saving, Environment and New Functional Materials
- Quantum Information and Micro-Nano Technology Applications
- Quantum Biomedical Technology
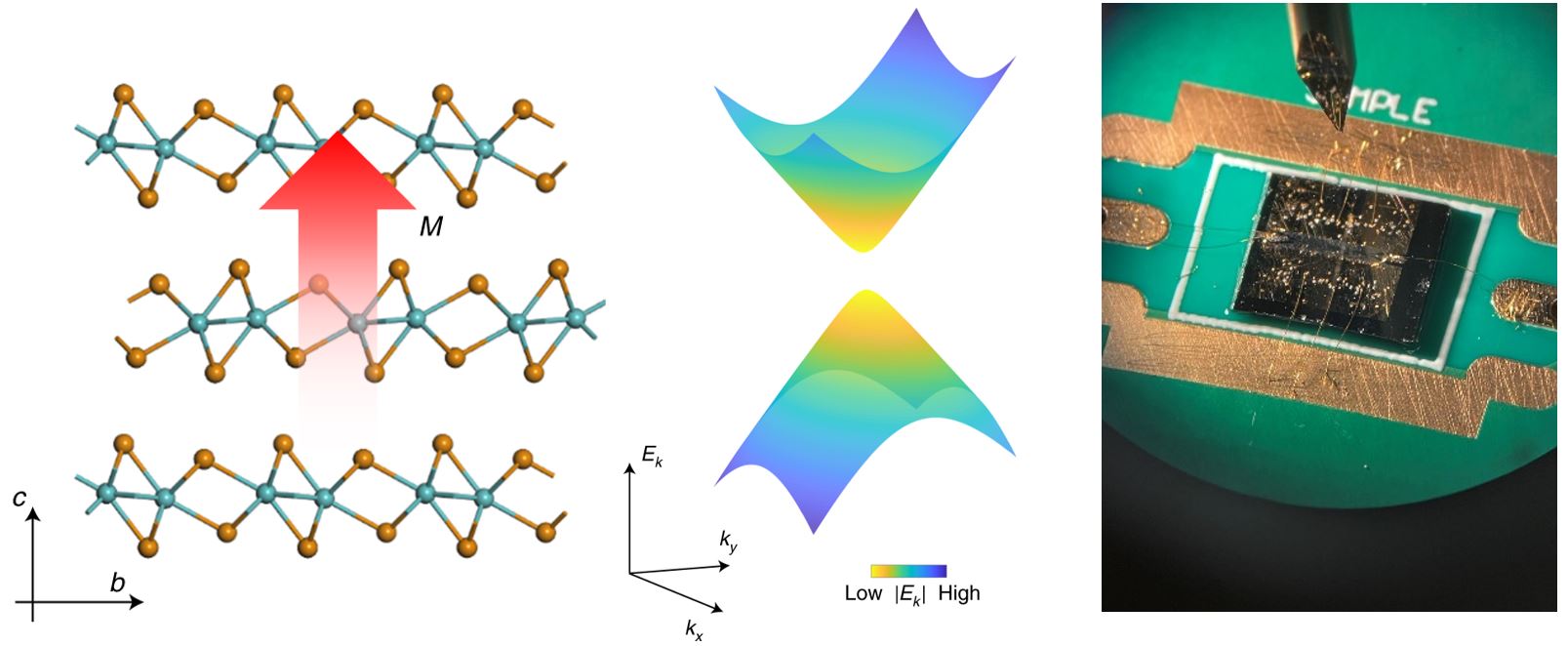
The research content of the Quantum Information mainly includes the following three aspects:
Quantum information and computation seeks to overcome the limitations of classical computing, achieving quantum supremacy in solving some classically hard problems and downgrading the algorithmic complexity from exponential to polynomial. We establish the quantum computing platform on superconducting qubit circuits and optical parametric oscillators. The former are nano-fabricated solid-state circuits using metal wires running in superconducting state, wherein the currents obey Josephson laws. The qubits containing these currents would exhibit superposition states, on which quantum algorithms can be executed concurrently to reduce algorithmic complexity. The latter are optical pulses that are scalable in optical ring cavity so that quantum entanglement needed by the quantum algorithms can be generated among two degrees of freedom on them.
Quantum nonlinear transport is an emerging research field of semiconductor physics, which involves diverse nonlinear transport phenomena of electrons induced from Berry curve, represented by the nonlinear Hall effect. Nonlinear Hall effect was first experimentally realized in 2019, and the study on this physical phenomenon all over the world are basically at the initial stage. Our works on nonlinear transport are focusing on the fundamental physics and the device applications.
In the field of theoretical study, we focus on various topological aspects in solid state systems, and the electronic, magnetic, transport, as well as optical properties of novel materials. The objective is not only to deepen the understanding of the fundamental physics, but also to enable the application of such understanding for the technological development. Various theoretical methods are used in the research, such as symmetry/topology analysis, semi-classical approach, tight-binding modeling, Green’s function method, first-principles DFT calculations, non-equilibrium Schwinger-Keldysh technique, scattering approach, and various kinds of numerical techniques.
Research Group Members
Zikang TANG
Chair Professor
SUN Handong
Distinguished Professor
Associate Director of IAPME
Hou IAN
Associate Professor
Coordinator of the Research Group
Shen LAI
Assistant Professor
Pengzhan SUN
Assistant Professor






